前回ご紹介した相模野基線は、一等三角点網図の基本となるものでした。
今回は、この基線を用いた三角測量について紹介します。

■ 三角測量の基礎

三角測量とは、三角形の1辺の長さとその両端の角度を観測して、正弦定理を用いて他の2辺の長さを計算で求めるものです。
ただし、高精度を必要とする基本測量や公共測量の場合は、すべての角度を観測し、内角の和が180度となるように調整してから、辺の長さを求めます。

かつては、下の写真のような「高覘標」と呼ばれるやぐらを立てて観測を行っていました。

「地図と測量の科学館」に展示されている高覘標（模型）

■ 三角測量の歴史

三角測量は、1617年、オランダの数学者であるスネリュウス（1570〜1626）により始まりました。
スネリュウスは、まず、オランダのハーグ〜ライデン間約15kmを結ぶ基線を設けます。
その後、教会にある塔を視準しながら南北に三角網を拡大し、ベルゲン〜アルクマール間の子午線弧長150kmを求めました。

■ 基線から始まる一等三角点網

相模野基線と日本経緯度原点から始まる一等三角点網は、次の手順で始まりました。

● 手順1
相模野基線を底辺（赤線）として、三角点「鳶尾山」と三角点「長津田村」を観測して相対的な位置を求めます。

● 手順2
「鳶尾山」と「長津田村」を結ぶ線を底辺（橙線）として、三角点「連光寺村」と三角点「浅間山」を観測して相対的な位置を求めます。

● 手順3
「連光寺村」と「浅間山」を結ぶ線を底辺（緑線）として、三角点「丹沢山」と三角点「鹿野山」を観測して相対的な位置を求めます。

● 手順4
「丹沢山」と「鹿野山」を結ぶ線を底辺（紫線）として、日本経緯度原点を観測して相対的な位置を求めます。

日本経緯度原点の経緯度はすでにわかっているので、これにより「丹沢山」と「鹿野山」の経緯度が確定します。
この三角形の各辺を基準とした一等三角点網が形成されました。

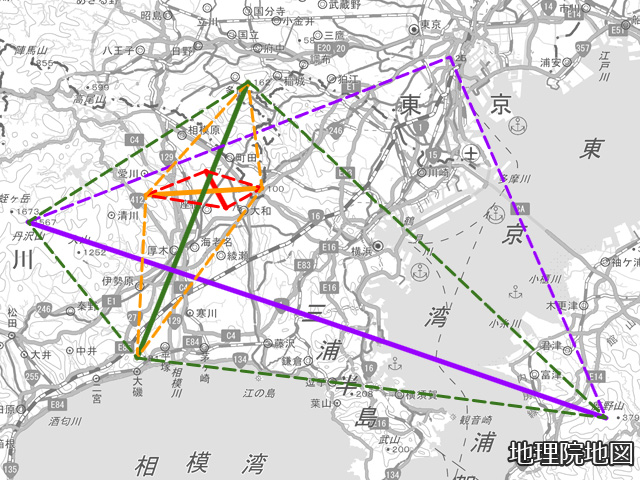
相模野基線から始まる一等三角網

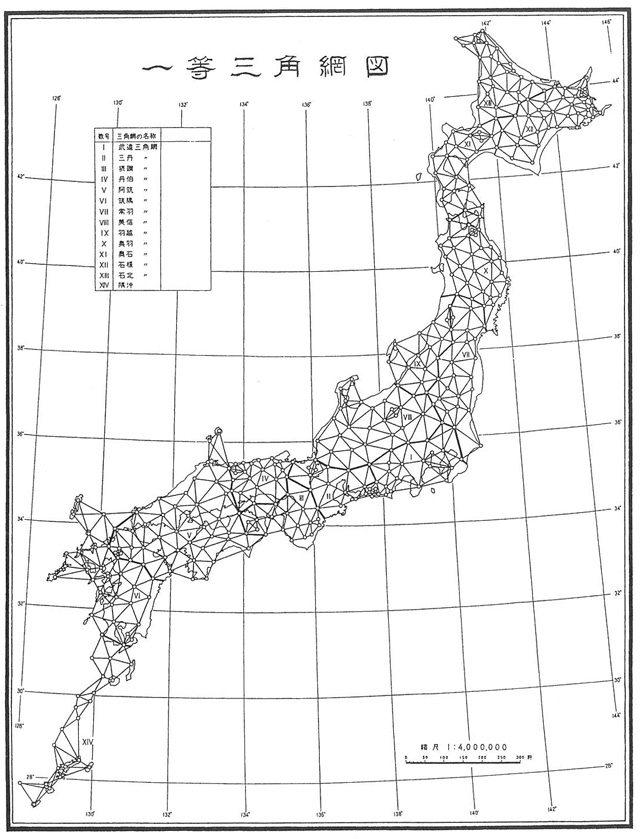
一等三角網図（出典：改訂2版 基礎測量学）

■ 三角測量から三辺測量へ

三角測量は明治以降の国家基準点の設置に用いられてきました。
1960年代になると光波測距儀が実用化され、距離観測精度が角観測精度より向上しました。
このため、三角測量は、辺長のみを観測する三辺測量に取って代わりました。

■ 参考文献

1) 長谷川昌弘・川端良和：改訂2版 基礎測量学, 電気書院, 2017.
2) 日本測量協会：測量士・測量士補国家試験受験テキスト, vol. 19, 2018.
3) 国土地理院ウェブサイト（https://www.gsi.go.jp/）
4) 地理院地図（https://maps.gsi.go.jp/）

測量・地図の仕事に興味があれば、まずは資料請求から始めませんか。
学校案内、募集要項ほか一式を無料で送付してます。

学校案内・募集要項の請求はバナーをクリック

オープンキャンパスは、測量・地図の仕事がわかる「体験入学」と学校がわかる「学校説明会」を開催中。
体験入学では在校生サポートがあるので、初めて測量に取り組む方でも安心してご参加いただけます。

日程・参加申込はバナーをクリック